Relation & Functions Chapter 2 Class 11

Relation & Functions

Basic concepts on relations and functions chapter 2 of class 11, basic point based on the topic relation and functions. Different types of functions and their graphs.

Introduction

In our daily life we come across different types of relations like brother and sister, father and son, husband and wife etc. 

Topics to be discussed Here

Ordered Pair Cartesian Product of two sets Relations complete explanations. Domain, Range and Co-domain of relations. Functions and Different types of functions. Graphs of the Functions. Undefined Terms.

Cartesian Product of two sets

If A and B are two sets then Cartesian product A X B is the set of all ordered pairs of elements from A to B, i.e.

          A X B = { (a, b) : a ∈ A, b∈ B }

First element of all the ordered pair  belongs to set A and second element belongs to set B.

If either A or B is a null set, then A X B will also be  empty set. In this case we can write A X B = φ

Ordered pair of elements:

An ordered pair of elements taken from two sets A and B is a pair of elements written in small brackets and grouped together in a particular order. i.e. (a, b).

Equal Ordered Pairs : 

Two ordered pairs are equal if and only if the corresponding first elements are equal and the second elements are also equal.

In general : 

Note:

i) If there are p elements in set A and q elements in set B, then there will be  pq elements in A X B.

 i.e. if n(A) = p and n(B) = q, then n(A x B) = pq.

ii) If A and B are non zero sets and either A or B  is an infinite set, then A X B is also an infinite set.

iii) A X A X A  = {(a, b, c) : a, b, c ∈ A }

Example :

Let A = {1, 2} and B = {3, 5, 8}, then

A X B = {1, 2} X {3, 5, 8}

          = {(1, 3), (1, 5), (1, 8), (2, 3), (2, 5), (2, 8)}

Here n(A) = 2, n(B) = 3,  n(A X B) = 6 = 2 x 3

⇒ n(A x B) = n(A) x n(B)

Relations

A relation R from set A to set B is the subset of Cartesian product A x B.

In Cartesian product A x B, number of relations equal to the number of subsets.

Domain

Set of all first elements of the ordered pairs in the relation R is called its domain.

Range

Set of all second elements of the ordered pairs in the relation R is called its range.

In any ordered pair second element is also called the image of first element.

Co-domain of the relation: 

The whole set B is called the co-domain of the relation R.

Example
In the above figure 
A X B = {(a₁, b₁), (a₁, b₂), (a₁, b₃), (a₂, b₁), (a₂, b₂), (a₂, b₃) }

Domain = {a₁, a₂ }

Range = { b₁, b₂, b₃}
n(A) = 2, n(B) = 3,  n(A X B) = 2 x 3 = 6
Number of subsets of A x B = 2⁶ = 64   
Number of relations of A X B = 2⁶ = 64   

Function their Domain, Range & Co-domain

Function

A relation is said to be a function If no two ordered pairs have same first element. A function from A to B is denoted by f : A→B

In a relation if different elements of set A has different images in set B then the relation is called a function

Example(1) :

f(x) = {(1, 2), (2, 3), (3, 4), (4, 5), (10, 20)}

Image of 1 = 2      ⇒ f(1) = 2

Image of 2 = 3      ⇒ f(2) = 3

Image of 3 = 4      ⇒ f(3) = 4

Image of 4 = 5      ⇒ f(4) = 5

Image of 10 = 20  ⇒ f(10) = 20

So different elements have different images, hence it is a function.

Example (2) :

f(x) = {(1, 2), (2, 3), (2, 4), (4, 5), (10, 20)}

Image of 1 = 2      ⇒ f(1) = 2

Image of 2 = 3      ⇒ f(2) = 3

Image of 2 = 4      ⇒ f(2) = 4

Image of 4 = 5      ⇒ f(4) = 5

Image of 10 = 20

Here we see that element 2 has two images 3 and 4, so it is not a function.

Domain of a function f : A→B

All those elements of set A which have their image in set B is called domain of a function.

Range of a function f : A→B

Set of all those elements of set B which have their pre-image in set A is called range of function.

Co-domain of a function f : A→B

Whole set B is called the co-domain

Real function and Real valued function: 

A function whose domain is either R or a subset of R then it is called a real  function. A function whose range is either R or a subset of R then it is called a real valued function.

Some Functions And Their Graphs

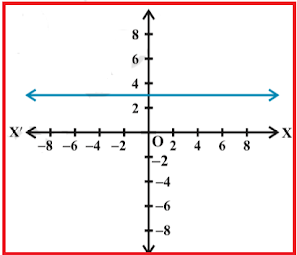
Constant Function :

A function f : R→ R defined by f(x) = c, where c is a constant is called a constant function

Domain = R or (-∞, ∞)

Range = {c} or [c, c]

For the constant function f(x) = c, the domain consists of all real numbers; there is no restrictions on the input. The only output value is the constant c, so the range is the set {c} that contains this single element. In interval notation, this is written as [c, c]. 

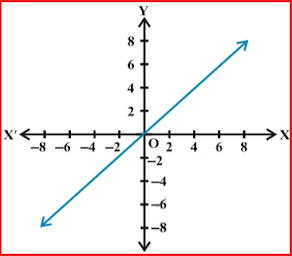
 Identity Function :

A function f : R→ R defined by f(x) = x is called an Identity function

Domain = R or (-∞, ∞)

Range = R or (-∞, ∞)

For the identity function f(x) = x, there is no restriction on x. Both domain and range are the set of all real numbers.

Modulus Function :

A function f : R→ R defined by  f(x) = |x| is called a modulus function.

Domain = R or (-∞, ∞)  and  Range = Positive Real Numbers including '0' or [0, ∞)

For the absolute value function f(x)=|x|, there is no restriction on x (domain). However, because absolute value is defined as a distance from 0, the output (range) can only be greater than or equal to 0.

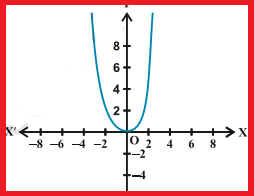
Quadratic polynomial  Function :

A function f : R → R defined by  f(x) = x²  is called a quadratic polynomial function.

Domain = R or (-∞, ∞)   

Range = Positive real numbers or  (0, ∞)

For the quadratic function f(x) = x², the domain is all real numbers because the horizontal extent of the graph is the whole real number line. Since the graph does not include any negative values for the range, the range is only non-negative real numbers.

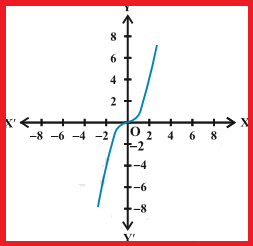
Cubic Polynomial  Function :

A function f : R→ R defined by  f(x) = x³  is called a Cubic Polynomial Function

Domain = R or (-∞, ∞) and  Range = R or (-∞, ∞)

For the cubic function f(x) = x³, the domain is all real numbers because the horizontal extent of the graph is the whole real number line. The same applies to the vertical extent of the graph, so the domain and range include all real numbers.

Reciprocal Function

A function defined by f(x) =    is called a reciprocal function

Domain = (-∞, 0) ⋃ (0, ∞) or  R - {0}

Range = (-∞, 0) ⋃ (0, ∞) or R - {0}

For the reciprocal function f(x)=  , we cannot divide any number by 0, so we must exclude 0 from the domain. Further, 1 divided by any value can never be 0, so the range also will not include 0. 

Reciprocal Squared Function

A function of the type f(x) =    is called a Reciprocal Squared Function.

Domain = (-∞, 0) ⋃ (0, ∞) or  R - {0}

Range = (0, ∞) or  Positive Real Numbers

For the reciprocal squared function f(x) =  , we cannot divide by 0, so we must exclude 0 from the domain. There is also no x that can give an output of 0, so 0 is also excluded from the range as well. Note that the output (Range) of this function is always positive due to the square in the denominator, so the range includes only positive Real numbers.

Square Root Function:

A function f(x) =  is called a square root function

Domain = [0, ∞)

Range = [0, ∞)

For the square root function f(x)= , we cannot take the square root of a negative real number, so the domain must be 0 or greater than "0". The range also excludes negative numbers because the square root of a positive number x is defined to be positive square root of negative number is negative.

Cube Root Functions

A function f(x) =   is called a cube root function.

Domain = R or (-∞, ∞)

Range =  R or (-∞, ∞)

For the cube root of a function f(x) =  , the domain and range include all real numbers. Note that cube root of positive number is positive and cube root of negative number is negative.

Signum Function :

The function f : R → R defined by 

 is called a signum function.

Domain of signum function is the set of real numbers.

Range of signum function is = {-1, 0, 1}

Graph of signum function is given below

Greatest Integer Function

The function f: R→ R defined by f(x) = [x], where x ∈ R, assumes the value of the greatest integer, less than or equal to x. This function is called the greatest integer function.

Domain of Greatest integer function is All real numbers.

Range of Greatest integer function = Set of all integers.

For examples [1.1] = 1,  [1.5] = 1,  [1.9] = 1

[5.3] = 5,   [5.8] = 5,  [-7.3]=-8,  [-7.9] = -8 

Undefined Terms : 

The terms like    are called the undefined terms. This situation is not valid for finding the limit of a function.

THANKS FOR YOUR VISIT

PLEASE COMMENT BELOW