Lesson Plan Math Class X (Ch-10) | Tangent To a Circle

E- LESSON PLAN   SUBJECT MATHEMATICS    CLASS 10

lesson plan for maths class X chapter 10 circle, lesson plans for mathematics teachers,  Method to write lesson plan for maths class 10, lesson plan for maths class X, lesson plan for mathematics grade X, lesson plan for maths teacher in B.Ed.

TEACHER'S NAME  :   Dinesh Kumar	SCHOOL :  RMB DAV CENTENARY PUBLIC SCHOOL NAWANSHAHR
SUBJECT   :   MATHEMATICS	CLASS                  :   X  STANDARD BOARD                 :  CBSE
LESSON TOPIC / TITLE   :  CHAPTER 10:  TANGENTS TO A CIRCLE	ESTIMATED DURATION:  This chapter is divided into Eight modules and it is completed in Ten class meetings.

TOPIC  Chapter 10 : Circle

DURATION

This topic is divided into Eight modules and are completed in ten class meetings.

PRE- REQUISITE KNOWLEDGE

Knowledge Properties of circle class 9^th

Knowledge of Pythagoras theorem.

TEACHING AIDS  Green Board, Chalk,  Duster, Charts  etc.

METHODOLOGY  Demonstration and Lecture method

LEARNING OBJECTIVES

• Definition of circle and the terms related to the circle like centre, radius, diameter, chord, segment and sector of the circle.

• Tangent to the circle at the point of contact, secant of the circle.

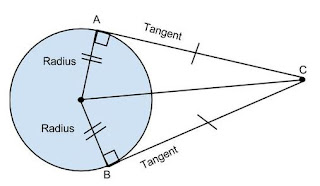
• (Prove) The tangent to the circle is perpendicular to the radius at the point of contact.

• (Prove) The length of the tangent to the circle from the external point are equal.

• (Motivate) Angle made by the chord of a circle with the tangent at the point of contact  is equal to the angle made by the chord in the alternate segment of the circle.

LEARNING OUTCOMES

• After studying this lesson students should know 
• the circle and the different terms associated with the circle. 
• Tangent and secant to the circle.
• Tangent is always perpendicular to the radius of the circle.
• Length of tangents from external point to the circle is always equal.
• Students should be able to apply all the results and concepts of circle  in the daily life problems problems.

RESOURCES

NCERT Text book of Mathematics

NCERT Exemplar Text Book

RESOURCE CENTRE at cbsemathematics.com

DAV Resource Material for class 10

KEY WORDS :

Similarity, congruency, Median, Orthocenter, Incentre, Altitude, Centroid, etc.

PROCEDURE

Start the session by checking their previous knowledge, by asking the questions related to the circle and the terms associated with it. Also explain the difference between the circle and sphere. After this introduce the topic circle step by step as follows.

S. No.	Explanation [For complete explanation of the topic]
1	Define  circle and the terms related to the circle like centre, radius, diameter, chord, segment and sector of the circle. Explain the topic diagrammatically and give some examples. Explain all the results associated with the circle that students had read in their 9th class.
2	Now define the term tangent and secant to the circle and explain the topic through their figures.
3	Now completely explain the theorem that radius is always perpendicular to the tangent at the point of contact. Also give its complete proof to the students.
4	Help the students by Solving  the problems based on the above theorem.
5	Now completely explain the theorem that length of tangent from external point to the circle are equal in length. Also give its complete proof to the students.
6	Help the students in solving the problems based on the above theorem.
7	Now explain the formula that relate the area and perimeter of the triangle with the radius of the in-circle. Also help the students in the implementation of this formula.
8	Now explain the statement of the theorem that angles in the alternate segment of the circle are equal. Also help the students in solving the problems based on this results.

MIND MAP ACTIVITY

STUDENTS DELIVERABLES:-

•  Review questions given by the teacher. 
• Students can prepare a presentation on circle which include all the important terms and results associated with the circle. 
• Solve NCERT problems with examples.
• Solve assignment given by the teacher.

EXTENDED LEARNING:

Students can extend their learning through the RESOURCE CENTRE and can find more valuable and interesting concepts on mathematics at  cbsemathematics.com

ASSESSMENT TECHNIQUES:

Assignment sheet will be given as home work at the end of the topic. Separate sheets which will include questions of logical thinking and Higher order thinking skills will be given to the above average students.

Class Test , Oral Test , worksheet and Assignments. can be made the part of assessment.

Re-test(s) will be conducted on the basis of the performance of the students in the test.

FEEDBACK:

All those students who performed well will be appreciated positively, and all those who can not perform up to the mark will again be given some important tips, guidance and  positive motivation to go through the topic again and then re-evaluated again. If possible then provision of remedial classes can be made for batter results.

THANKS FOR YOUR VISIT

PLEASE COMMENT BELOW

🙏