Properties of the circle

Properties of the circle

Circle properties and formulas, properties of circle class 10, properties of circle class 9, easy definition of circle, types of circle, tangent, secant to the circle, cyclic quadrilateral and its properties.

In this chapter we will discuss the following:

Definition of Circle, Radius, Diameter, Chord, Segment, Sector, Cyclic Quadrilateral, their Definitions, Properties of Circle, Properties of Cyclic Quadrilateral with complete explanations.

CIRCLE:-
Collection of all points in a plane which are at the equidistant from the fixed point, is called a circle.

The fixed point is called centre and fixed distance is called radius.

RADIUS:-
A line segment which join the centre with any point on the circle is called radius.

DIAMETER:-
A line segment which join any two points on the circle and is passes through the centre of the circle  is called the diameter of the circle.
Diameter is the double of radius.
Longest chord of the circle is called its diameter.

CHORD:-
Any line segment which join any two points on the circle is called its chord.
Diameter of the circle is also the chord of the circle.

SECTORS:-

Area between the radius and arc is called sector of the circle.
Sectors are of two types: Minor sector and Major Sector
Minor Sector : Smaller sector is called minor sector.
Major Sector : Larger area is called major sector.

SEGMENT :-

Area between the chord and arc is called segment.
Segments are of two types : Minor Segment and Major Segment.
Minor Segment : Smaller area is called minor segment.
Major Segment : Larger area is called major segment.

PROPERTIES OF CIRCLE:-

• Equal chords of the circle subtend equal angles at the centre of the circle.
• If two chords subtend equal angles at the centre of the circle then the chords are equal.

If AB = CD then ㄥAOB = ㄥCOD

• There is only one circle passes through the three non-collinear point.

-

• Two circles can intersect each other at the most two points.

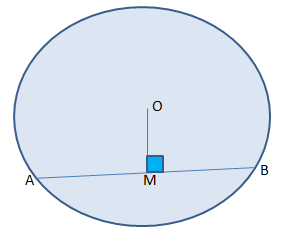
• Perpendicular from the centre to the chord bisect the chord.



If OM 丄 AB, then AM = BM

If AM = BM, then, OM 丄 AB

• A line segment joining centre of the circle with the mid - point of the chord is perpendicular to the chord.

• Angle made by an arc at the centre is double the angle  made by the same arc in the remaining part of the circle. 
  

ㄥBOC = 2ㄥBAC

• Angles in the same segment of the circle are equal. 

ㄥC = ㄥD = ㄥE = ㄥF

CYCLIC QUADRILATERAL:-
A quadrilateral whose all vertices lie on the circle is called a cyclic quadrilateral.

PROPERTIES OF CYCLIC QUADRILATERAL:-
Opposite angles of a cyclic quadrilateral are supplementary (180 degree).

ㄥA + ㄥC = 180^o  ,   ㄥB + ㄥD = 180^o

                                 

Exterior angle of a cyclic quadrilateral is equal to the interior opposite angle.
                                                      ㄥCBE = ㄥD

TANGENTS TO A CIRCLE

Tangent Line
If a line touch the circle at one point then it is called tangent to the circle.

Secant Line :
If a line intersect the circle at two points then the line is called section.

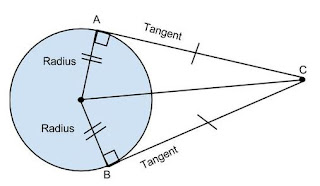
PROPERTIES OF TANGENT TO THE CIRCLE

Tangent is always perpendicular to the radius of the circle.

       

Length of the tangents from the exterior points to the circle are equal.

                            

Important Result

Relation between Area and Perimeter of a triangle with the radius of incircle

Incircle :-  It is the circle inscribed inside the triangle whose centre is at equidistant from the sides of the triangle.

\[\frac{Area\; of\; triangle}{semi\; \; perimeter\; of\; the\; triangle}=Radius\; of\; the\; in circle\]

Algorithm to solve such problems

1) Find the perimeter of the triangle and then semi-perimeter.

2) Find area of the triangle. If it is an isosceles triangle then use Heron's Formula.

3) Use the above formula to find the required result. 

PROOF OF IMPORTANT THEOREMS ON THE CIRCLE

THEOREM 10.1 CHAPTER 10 CLASS 10

Statement :

Tangent is always perpendicular to the radius at the point of contact.

Given: In circle C(o,r), XY is tangent to the circle at point P.

To Prove:  OP ⊥ XY

Construction : 

Take any arbitrary point Q (other than P ) on the line XY and join OQ which meet the circle at point R.

Proof:

In order to prove that OP ⊥ XY it is sufficient to prove that OP is the smallest line segment than all the line segments  obtained by joining O with any point on XY.

OP = OR .......... (Equal radii)

Now OQ = OR + RQ

OQ = OP + RQ

Subtract RQ from the R.H.D. we get

OQ > OP or

OP < OQ

But Q is an arbitrary point on XY

⇒ OP is the smallest line segment and smallest line segment is always perpendicular.

Hence OP ⊥ XY

Hence prove the required theorem

  

    

THEOREM 10.2  CHAPTER 10 CLASS 10

Statement

Prove that length of tangents from external point to the circle are equal in length.

Given : AC and BC are two tangents from external point to the circle.

To Prove : AC = BC

Construction:  Join OA, OB and OC

Proof:

Since radius is always perpendicular to the tangent.

∴ ㄥ1 = ㄥ2 = 90^o

In ΔAOC and ΔBOC
OA = OB ............... (Equal radii)
OC = OC .............. (common side)
ㄥ1 = ㄥ2 .............. (Each = 90o 
∴ By RHS ≌ rule
ΔAOC ≌ ΔBOC 
⇒ AC = BC .............By CPCT
Hence prove the required result 

Results of other important theorems on circle

Angle made by the chord of the circle with the tangent of the same circle (at the point of contact of the chord and tangent) is equal to the angle made by the chord in the alternate segment of the circle. 

If AB and CD are two chords of the circle intersect each other at point p inside or outside  the circle then:- 

PA X PB = PC X PD

 

        Inside the circle                                                                                         Outside the circle

If chord AB of a circle intersect the tangent of the same circle at point P outside the circle then 

PA X PB = PT²

THANKS FOR YOUR VISIT

PLEASE VISIT AGAIN

🙏

CIRCLE - CBSE Mathematics