Three Dimensional Geometry Class XII Chapter 11

Three Dimensional Geometry Class XII Chapter 11

Basic concepts and formulas of 3D-Geometry class XII chapter 11, Equations of line and plane in space, shortest distance between skew lines, angle between two lines and planes.

 Introduction:

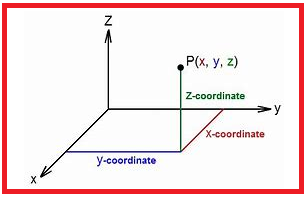
It is that branch of mathematics in which we discuss the point, line and plane in the space. 

We got a little introduction of 3 dimensional -Geometry in class 11 chapter 12.

Here in class XII we make use of vector algebra in 3 dimensional - Geometry. 

In this chapter we discuss the following points.

• Direction angles, 
• Direction cosines 
• Direction ratios. 
• Equation of line passing through one point, two point.
• Angle between two lines, parallel lines and perpendicular lines.
• Shortest distance between two lines.
• Collinearity of two lines.
• Equation of plane passing through  one point and through three points.
• Angle between two planes.
• Distance of the plane from the point.
• Angle between  line and plane.

Direction angles: 

These are the angles made by the vector with the positive direction of the axis. These are denoted by α, β, 𝜸

Direction cosines: 

Cosines of the direction angles are called direction cosines.

If α, β, 𝜸 are the direction angles made by a vector with the axis then cosα, cosβ, cos𝜸 are called the direction cosines. These are also denoted by l, m, n

l = cosα,  m = cosβ,  n = cos𝜸

If l, m, n are the direction cosines of a line then   l² + m² + n² = 1

Direction ratios: 

The terms which are proportional to the direction cosines are called direction ratios. These are denoted by  (a, b, c)

For Example: 

Let any vector given by : 

Its magnitude is given by 

(a, b, c) are the direction ratios and the direction cosinesl, m, n  are given by 

If  ɑ, 𝛃, 𝛄 are the direction angles made by the line with positive direction of x-axis, y-axis, z-axis then cosɑ , cos𝛃 , and cos𝛄 are called the direction cosines of that line. These are also be denoted by l, m, n such that 

*******************************************

EQUATION OF  LINES IN SPACE

**********************************************

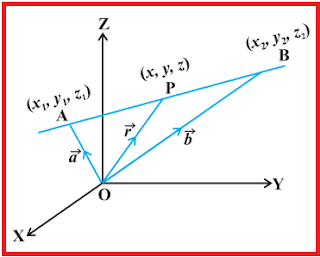
Case I : Equation of a line passing through the point A(x₁, y₁, z₁) and is parallel to vector b is given by

In vector form equation of line is  

Where: 

In cartesian form

Case II : Equation of a line passing through the two points.

Let given equation passes through the two points A(x₁, y₁, z₁) and B(x₂, y₂, z₂). Let P(x, y, z) is any arbitrary point on the line.

Then equation of line  is given by 

In vector form equation of line is:      

Where: 

In cartesian form equation of line is

***********************************

Angle between two lines

In Vector form let two equations of lines are

and let θ is the angle between these two lines then we have 

 

In cartesian form let two equations of line are

 

 

Two lines are perpendicular if   

Two lines are parallel if    

Skew lines:

In space there are lines which are neither parallel nor intersecting such lines are non-coplanar and are called skew lines.

Shortest Distance between two lines

If two lines in space intersect each other then shortest distance between them = 0, 

If two lines in one plane are parallel then shortest distance is the perpendicular distance between them.

Let two skew lines in vector form are \[\overrightarrow{r}=\overrightarrow{a_{1}}+\lambda \overrightarrow{b_{1}}\; and\; \overrightarrow{r}=\overrightarrow{a_{2}}+\lambda \overrightarrow{b_{2}}\]Shortest distance between two lines is 

\[d=\left | \frac{\left (\overrightarrow{a_{2}}-\overrightarrow{a_{1}} \right ).\left ( \overrightarrow{b_{1}}\times \overrightarrow{b_{2}} \right )}{\left |\overrightarrow{b_{1}}\times \overrightarrow{b_{2}} \right |} \right |\]

Coplanarity of two lines: Two lines are coplanar if 

\[\left (\overrightarrow{a_{2}}-\overrightarrow{a_{1}} \right ).\left ( \overrightarrow{b_{1}}\times \overrightarrow{b_{2}} \right )=0\]

In cartesian form two lines are coplanar if 

\[ \left | \begin{matrix} x_{2}-x_{1} &y_{2}-y_{1} &z_{2}-z_{1} \\ a_{1}&b_{1} &c_{1} \\ a_{2} &b_{2} &c_{2} \end{matrix} \right |=0\]

Here shortest distance between two lines become = 0 and the lines are coplanar lines or intersecting lines.

Distance between two parallel lines

Two lines are parallel when their direction vectors are same. 

When two lines are parallel then they are coplanar lines.

Let two parallel lines are \[\overrightarrow{r}=\overrightarrow{a_{1}}+\lambda \overrightarrow{b_{1}}\; and\;\overrightarrow{r}=\overrightarrow{a_{2}}+\lambda \overrightarrow{b_{2}}\]\[When\; two\; lines\; are\; parallel\; then\; \; \overrightarrow{b_{1}} =\overrightarrow{b_{2}}=\overrightarrow{b}\]

Then shortest distance between two parallel lines is 

\[d=\left |\frac{ (\overrightarrow{a_{2}}-\overrightarrow{a_{1}})\times \overrightarrow{b}}{\left | b \right |} \right |\]

**************************************************

THREE DIMENTINAL GEOMETRY PLANE

A plane is determined uniquely if any one of the following is known. 

a) When normal to the plane and its distance from the origin is given. That is equation of the plane in Normal form.

b) When it passes through a point and is perpendicular to the given direction.

c) It passes through the three non- collinear points.

Normal form of equation of Plane

Let us consider a plane whose ⟂ distance from the origin is d. Let P(x, y, z) is any arbitrary point in the plane whose position vector from the origin is vector r.

Equation of plane in normal form is given as 

\[In\: vector\: form\: \:\; \vec{r}.\hat{n}=d,\: \:\]

Where: \[\vec{r}=x\hat{i}+y\hat{j}+z\hat{k}\]\[\hat{n}=l\hat{i}+m\hat{j}+n\hat{k}\]here l, m, n are the direction cosines of the normal vector N.

Equation of plane in cartesian form is \[(x\hat{i}+y\hat{j}+z\hat{k}).(l\hat{i}+m\hat{j}+n\hat{k})=d\]

\[lx+my+nz=d\]

[lx+my+nz=d\]

Equation of the plane perpendicular to the given vector and passing through a given point.

There are many planes which are perpendicular to the given vector as shown in the figure.

 but there is only one plane which is perpendicular to the given vector and is passes through the given point.

Let a plane passes through the point A with position vector a and is ⊥ to a vector N.

Let P(x,y,z) is an arbitrary point in the plane

In triangle AOP by triangle law of vector addition we have 

\[\overrightarrow{OA}=\overrightarrow{OP}+\overrightarrow{AP}\]\[\overrightarrow{AP}=\overrightarrow{OP}-\overrightarrow{OA}\]\[\overrightarrow{AP}=\overrightarrow{r}-\overrightarrow{a}\]Vector N is a normal vector to the plane and is always perpendicular to the plane and vector AP is a vector in the plane so vector AP is always ⊥ to the normal vector of the plane. When two vectors are ⊥ then their dot product is zero. 

\[(\vec{r}-\vec{a}).\vec{N}=0,\; \Rightarrow \; \vec{r}.\vec{N}-\vec{a}.\vec{N}=0\Rightarrow \vec{r}.\vec{N}=d\]

\[Where\; \; \vec{a}=x_{1}\hat{i}+y_{1}\hat{j}+z_{1}\hat{k}\; \; is\; the\; position\; vector\; of\; a\; point\; in\; the\; plane\]\[\vec{N}=a\hat{i}+b\hat{j}+c\hat{k}\: is\: a\: vector\: perpendicular\; to\; the\; plane\]

Equation of the plane passing through the three non- collinear points.

Let vector a, vector b and vector c are three non-collinear vectors in the plane and let P(x, y, z) is any arbitrary point in the plane. Then equation of plane passing through these three points is given by 

\[\overrightarrow{AB}\times \overrightarrow{AC}\;\; is \; a \; vector\; \perp\; to\; the\; plan\; and\; \; \overrightarrow{AP} \;\; lie \; in\; the\; plane\]\[So\; equation\; of\; the\; plane\; is\; given\; by\; \; \overrightarrow{AP}.[\overrightarrow{AB}\times \overrightarrow{AC}]\]\[Where \; \; \overrightarrow{AP}=\vec{r}-\vec{a},\; \; \overrightarrow{AB}=\vec{b}-\vec{a},\; \; \overrightarrow{AC}=\vec{c}-\vec{a}\] Putting these values,  the equation of the plane becomes

\[(\vec{r}-\vec{a}).[(\vec{b}-\vec{a})\times (\vec{c}-\vec{a})]=0,\]

Where: \[\vec{r}=x\hat{i}+y\hat{j}+z\hat{k},\: \: \vec{a}=x_{1}\hat{i}+y_{1}\hat{j}+z_{1}\hat{k}\\\vec{b}=x_{2}\hat{i}+y_{2}\hat{j}+z_{2}\hat{k},\: \: \vec{a}=x_{3}\hat{i}+y_{3}\hat{j}+z_{3}\hat{k}\] In cartesian form equation of the plane passing through three points (x₁, y₁, z₁), (x₂, y₂, z₂), (x₃, y₃, z₃) is given by 

\[\left | \begin{matrix} x-x_{1} &y-y_{1} &z-z_{1} \\ x_{2}-x_{1}&y_{2}-y_{1} &z_{2}-z_{1} \\ x_{3}-x_{1}& y_{3}-y_{1} &z_{3}-z_{1} \end{matrix} \right |=0\]

If we apply the above formula and we get 0 = 0 ⇒ three points are collinear.

If three points are collinear then there are many planes passing through three points. 

Intercept form of equation of line: 

\[\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1\]

Where a, b, c are the intercepts made by the plane on the x-axis, y-axis, z-axis respectively.

Equation of the plane passing through the intersection of two planes.

In Vector form: Let equation of two panes are\[\vec{r}.\hat{n}_{1} = d_{1}\: \: and\: \:\vec{r}.\hat{n}_{2} = d_{2}\]Equation of any plane passing through the intersection of these two planes is given by

\[\vec{r}.(\hat{n}_{1}+\lambda \hat{n}_{2}) = d_{1}+\lambda d_{2}\]

If equation of two planes are \[\vec{r}.\overrightarrow{N_{1}} = d_{1}\: \: and\: \:\vec{r}.\overrightarrow{N_{2}}=d_{2}\]Equation of any plane passing through the intersection of these two planes is given by

\[\vec{r}.(\vec{N}_{1}+\lambda \vec{N}_{2})=d_{1}+\lambda d_{2}\]

 In cartesian form let equation of  two planes are \[a_{1}x+b_{1}y+c_{1}z-d_{1}=0\: \: and\: \: a_{2}x+b_{2}y+c_{2}z-d_{2}=0\]Equation of any plane passing through the intersection of these two planes is given by

\[(a_{1}x+b_{1}y+c_{1}z-d_{1}) + \lambda ( a_{2}x+b_{2}y+c_{2}z-d_{2})=0\]

Angle between two planes

Let equations of two planes are\[\vec{r}.\vec{N}_{1}=d_{1}\: \: and \: \: \: \vec{r}.\vec{N}_{2}=d_{2}\]If θ is the angle between then

\[cos\theta =\left |\frac{\overrightarrow{N_{1}}.\overrightarrow{N_{2}}}{|\overrightarrow{N_{1}}||\overrightarrow{N_{2}}|} \right |\\\]

In cartesian form angle between two planes is given by 

\[cos\theta =\left |\frac{a_{1}a_{2}+ b_{1}b_{2} +c_{1}c_{2}}{\sqrt{(a_{1}^{2}+b_{1}^{2}+c_{1}^{2})(a_{2}^{2}+ b_{2}^{2}+ c_{2}^{2})}} \right |\]\[Two\: lines\: are\: perpendicular\: \: if\: \: {a_{1}a_{2} +b_{1}b_{2}+c_{1}c_{2}}=0\]\[Two\: lines\: are\: Parallel\: \: if\: \: \frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\]

Distance of a point from the plane

Distance of a point A(x₁, y₁, z₁) from the plane ax + by + cz = d is

\[D=\left | \frac{ax_{1}+by_{1}+cz_{1}-d}{\sqrt{a^{2}+b^{2}+c^{2}}} \right |\]

In vector form

\[D=\left | \frac{\vec{a}.\vec{N}-d}{|\vec{a}|} \right |,\: \: where\: \vec{a}=x\hat{i}+y\hat{j}+z\hat{k}\]

********************************

Angle between a line and a plane

\[Let \: \: equation \: \: of\: \: line\: \: is\: \: \vec{r}=\vec{a}+\lambda \vec{b}\: \: and\\Equation\: \: of\: plane\: \: is\: \: \vec{r}.\vec{N}=d\]Then angle between the line and plane is the complement of the angle between the line and normal to the plane . If θ is the angle between line and normal to the plane then \[cos\theta =\left | \frac{\vec{b}.\vec{N}}{|\vec{b}||\vec{N}|} \right |\]If θ is the angle between line and normal to the line then   90-θ is the angle between line and the plane.

\[cos(90-\theta )=sin\theta =\left | \frac{\vec{b}.\vec{N}}{|\vec{b}||\vec{N}|} \right |\]

Thanks for your visit

Please comment below