Three Dimensional Geometry Class 11 | Ch-11

Three Dimensional Geometry

Basic concepts of three dimensional geometry class 11 , Distance formula , section formula, mid-point formula and centroid of triangle

Introduction :

 To locate the position of a point in a plane we need two intersecting mutually perpendicular lines in the plane. 

 

These lines are called coordinate axis and the two points in this case are called the coordinates of the point with respect to the axis.

 

To locate the position of an object in a space we need three mutually perpendicular planes. These planes are called three coordinate planes.  

 

Three numbers representing the three distances of an object from three coordinate planes are called the coordinates of the point on the object.

So any point in space has three coordinates.

 

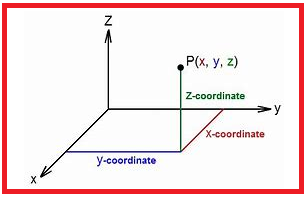
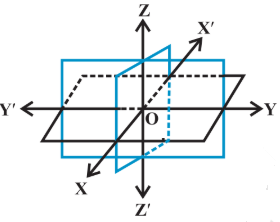
Coordinate axis and coordinate planes in three dimensional planes

Coordinate axis in two dimensions divide the plane into four quadrants.   

In three dimensions coordinate planes divide the space(three dimension) into eight parts and each part is called octant, as shown in the figure.

Three Mutually Perpendicular Planes

Rectangular Coordinate System 

With the help of quadrants we can make the sign convention for octant as follows.

Cartesian Coordinate System

For x-axis  and y-axis Sign convention in different quadrant is given as above.

In three dimension we have one more axis that is z-axis. 

For first four octant (I to IV) we take the sign of x-axis and y-axis same  as it is in quadrant I to IV and the sign of z-axis is taken positive. 

For Example

In first octant : x-axis is +ve, y-axis is +ve and z-axis is also +ve. So in first octant point is of the form (+, +, +)

In second octant : x-axis is -ve, y-axis is +ve and z-axis is  +ve. So in second octant point is of the form (-, +, +) and so on up to 4th octant.

For last four octant (V to VIII) we again  take the sign of x-axis and y-axis as given in quadrant  I to IV  and sign of z-axis is taken negative.

For Example

In 5th octant : x-axis is +ve, y-axis is +ve and z-axis is  -ve. So in 5th  octant point is of the form (+, +, -)

In 6th octant : x-axis is -ve, y-axis is +ve and z-axis is  -ve. So in 6th  octant point is of the form (-, +, -) and so on up to VIII octant.

So sign convention for eight octant is written as

Octant	I	II	III	IV	V	VI	VII	VIII
Sign	(+,+,+)	(-,+,+)	(-,-,+)	(+,-,+)	(+,+,-)	(-,+,-)	(-,-,-)	(+,-,-)

In Three dimensions:

Coordinates of the point on x-axis is (x, 0, 0), 

Coordinates of the point on y-axis is (0, y, 0), 

Coordinates of the point on z-axis is (0, 0, z),

Coordinate of the point in xy-plane is of the form (x, y, 0), 

Coordinate of the point in yz-plane is of the form (0, y, z), 

Coordinate of the point in zx-plane is of the form (x, 0, z),

Coordinates of a point in space is of the form (x, y, z)

Distance Formula

Distance between two points P(x₁, y₁, z₁) and Q(x₂, y₂, z₂) is given by \[|PQ|=\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}+(z_{2}-z_{1})^{2}}\]

Types of Quadrilaterals By using Distance formula

Let ABCD is a quadrilateral. Then with the help of distance formula find the length of sides |AB|, |BC|, |CD|, |DA| and diagonals |AC|  and |BD|

i) If opposite sides are equal but diagonals are not equal then quadrilateral is a parallelogram. or |AB| = |CD|, |BC| = |DA| and |AC| ≠ |BD|

ii) If opposite sides are equal and diagonals are also equal then quadrilateral is a Rectangle. or |AB| = |CD|, |BC| = |DA| and |AC| = |BD|

iii) If all sides are equal and diagonals are not equal then quadrilateral is rhombus. or  |AB| = |BC| = |CD| =  |DA| and |AC| ≠ |BD|

iv) If all sides are equal and diagonals are also equal then quadrilateral is square. or |AB| = |BC| = |CD| =  |DA| and |AC| = |BD|

v) If two pair of adjacent sides are equal and diagonals are not equal then quadrilateral is a Kite.

Section Formula:

Here two cases are arises

1. If Point P(x, y, z) divide the  line through the points A(x₁, y₁, z₁) and B(x₂, y₂, z₂) in ratio m₁ : m₂  internally, then coordinates of point P are given by section formula:

\[P(x,y,z)=\left ( \frac{m_{1}x_{2}+m_{2}x_{1}}{m_{1}+m_{2}}, \frac{m_{1}y_{2}+m_{2}y_{1}}{m_{1}+m_{2}}, \frac{m_{1}z_{2}+m_{2}z_{1}}{m_{1}+m_{2}} \right )\] 

2. If Point P(x, y, z) divide the  line through the points A(x₁, y₁, z₁) and B(x₂, y₂, z₂) in ratio m₁ : m₂  Externally, then coordinates of point P are given by section formula:

\[P(x,y,z)=\left ( \frac{m_{1}x_{2}-m_{2}x_{1}}{m_{1}-m_{2}}, \frac{m_{1}y_{2}-m_{2}y_{1}}{m_{1}-m_{2}}, \frac{m_{1}z_{2}-m_{2}z_{1}}{m_{1}-m_{2}} \right )\] 

Mid-Point formula:

If Point P(x, y, z) is the mid-points of the line joining the points A(x₁, y₁, z₁) and B(x₂, y₂, z₂) then\[P(x,y,z)=\left ( \frac{x_{1}+x_{2}}{2},\frac{y_{1}+y_{2}}{2},\frac{z_{1}+z_{2}}{2} \right )\]

 Median:

Median is the line segment which join the vertex of the triangle with the mid-point of the opposite side.

 

Centroid:

Point of concurrence of all the median of the triangle is called its centroid

Centroid of the triangle whose vertices are A(x₁, y₁, z₁),  B(x₂, y₂, z₂)  and C(x₃, y₃, z₃) is given by\[P(x,y,z)=\left ( \frac{x_{1}+x_{2} +x_{3}}{3},\frac{y_{1}+y_{2}+y_{3}}{3}, \frac{z_{1}+z_{2}+z_{3}}{3} \right )\]Centroid of the triangle divide the median in 2 : 1

 

Centroid of the given triangle and the triangle obtained by joining the mid-points of the sides of the triangle are same.

THANKS FOR YOUR VISIT 

PLEASE COMMENT BELOW

🙏