Relation and Functions Class XII Chapter 1

Class 12  chapter 1
Relations and functions

Basic concepts of topic relations and functions class XII chapter 1 of mathematics. Equivalence relations, different types of functions, composition and inverse of functions.

Introduction

In class 11 we have studied about Cartesian product of two sets, relations, functions, domain, range and co-domains. Now in this chapter we have studied about the different types of relations, different types of functions, composition of functions and invertible functions.

Relations

A relation R from set A to set B is the subset of Cartesian product A x B.

In Cartesian product A x B number of relations equal to the number of subsets.

Domain

Set of all first elements of the ordered pairs in the relation R is called its domain.

Range

Set of all second elements of the ordered pairs in the relation R is called its range.

In any ordered pair second element is also called the image of first element.

Types of relations

i) Empty Relation:

A relation R in set A is called empty relation, if no element of A is related to any element of A, i.e., R = φ  ⊂ A x A

Example: 

Let A = {1, 2, 3} and R be a relation on the set A defined as R = {(a, b) : a + b = 10; a, b ∈ A}

Here R is empty relation. R = Φ

ii) Identity Relation

A relation R in set A is called identity relation, if every element of A is related to itself, i.e., R = (a, a)  ⊂ A x A

A relation R is an identity relation in set A if for all a ∈ A, (a, a) ∈ R.

iii) Universal Relation :

A relation R in a set A is called universal relation, if each element of A is related to every element of A, i.e., R = A x A

iv) Reflexive relation

A relation R in a set A is called reflexive, if (a, a) ∈ R,  for every a ∈ A

Number of reflexive relations

The number of reflexive relations on a set with n elements is given by N =   

Example

If n(A) = 5, the number of reflexive relations in a set A = 2^5(5-1) = 2^5x4 = 2²⁰.
If n(A) = 3, the number of reflexive relations in a set A = 2^3(3-1) = 2^3x2 = 2⁶ = 64.

v) Symmetric Relation

A relation R in a set A is called symmetric, if (a, b) ∈R implies that (b, a) ∈ R, for all a, b ∈ A.

Number of Symmetric Relations

Number of Symmetric Relations on a set is given by N = , where N is the number of symmetric relations and n is the number of elements in the set,

Example

If n(A) = 3, then number symmetric relations are given by 

vi) Transitive Relation

A relation R in a set A is called transitive, if (a, b) ∈R and (b, c) ∈R, implies that (a, c) ∈ R, for all a, b, c ∈ A
Number of Transitive Relations

To find the number of Transitive Relations, there is no implicit formula yet discovered.

However number of Transitive Relations for the set having number of elements from 0 to 6 are given below.

Number of elements	Number of Transitive relations
0	1
1	2
2	13
3	171
4	3994
5	154303
6	9415189

 

vii) Equivalence relation:

A relation R in set A is said to be equivalence relation if it is reflexive, symmetric  and transitive relation.

Number of equivalence relations

Number of equivalence relations can be calculated as follows

For one element:            1

For two Elements:           1            2

For three Elements :       2            3            5

For four Elements :         5            7           10         15

For five Elements :          15         20         27         37              52

For six Elements :           52         67         87         114            151       203

Number of elements	No. of equivalence relations
1	1
2	2
3	5
4	15
5	52
6	203

Viii) Equivalence Class:

Let R be an equivalence relation on a set A and let a ∈ A. Then we define equivalence class of a as 

[a] ={b ∈ A : b is related to a} = {b ∈ A : (b, a) ∈ R}

Note : Both empty relation and universal relations are sometimes called equivalence relation of trivial relation.

The empty relation on a nonempty set is symmetric and transitive, but it's not reflexive. 

The empty relation on the empty set is reflexive, symmetric, and transitive. It's an equivalence relation

An Empty relation R on the non-empty set S is not an equivalence relation

Explanation:

Reflexivity fails because no element in set S is related to itself (since the relation is empty, there are no pairs at all).

Symmetry and Transitivity are vacuously true for the empty relation, because there are no pairs to contradict these properties. However, reflexivity is a necessary condition for a relation to be an equivalence relation, and since the empty relation does not satisfy reflexivity, it cannot be considered an equivalence relation.

An Empty relation R on the empty set S is an equivalence relation

Explanation

Reflexivity

A relation R on a set S is reflexive if every element a ∈ S  is related to itself, i.e., (a, a)∈R  for all a ∈ S .

Since S is empty, there are no elements a ∈ S that need to satisfy (a, a)∈R. Hence, the reflexivity condition is vacuously true.

Symmetry

A relation R on a set S is symmetric if for all a, b ∈ S, whenever (a, b)∈R, it follows that (b, a) ∈ R.

Since S is empty, there are no pairs (a, b) to consider. Hence, the symmetry condition is vacuously true.

Transitivity

A relation R on a set S is transitive if for all a, b, c ∈ S, whenever (a, b)∈R and (b, c)∈R, it follows that (a, c)∈R.

Since S is empty, there are no pairs (a, b) and (b, c) to consider. Hence, the transitivity condition is vacuously true.

Since the empty relation on the empty set vacuously satisfies reflexivity, symmetry, and transitivity, it is indeed an equivalence relation.

Vacuously true :

A statement is said to be "vacuously true" if it is true in a trivial way due to the fact that there are no instances to disprove it or if there is no counter example to disprove it.

Trivial:

In mathematics and logic, "trivial" typically refers to something that is simple, straightforward, or self-evident. A trivial case is often one that is so simple or obvious that it doesn't require much proof or explanation. 

Trivial Relation

A trivial relation in the context of set theory and relations typically refers to one of two specific relations on a set:

1. Empty Relation: This is the relation where no element is related to any other element, including itself. Formally, for a set S, the empty relation R is defined as R = ∅. In other words, (a, b) ∉ R for any a, b ∈ S in S.
2. Universal Relation: This is the relation where every element is related to every other element, including itself. Formally, for a set S, the universal relation R is defined as R = S × S. In other words, (a, b)∈R for all a, b ∈ S. 

Examples of relations
(i) Symmetric but neither reflexive nor transitive.

Let relation is defined on A = {1, 2}

Answer: R = { (1, 1), (1, 2), (2, 1)}

(1, 2), (2, 1) ∈ R, so it is symmetric relation.

(2, 2) ∉ R so it is not reflexive.

(2,1) ∈ R and (1, 2) ∈ but (2, 2) ∉ R , so it is not transitive.

(ii) Transitive but neither reflexive nor symmetric.

Let a relation R is defined on a set A = {1, 2, 3}

Answer: {(1, 3)} 

(1, 3) ∈ R and there is no ordered pair whose first element is 3, so it is a transitive relation.

(1, 1), (2, 2), (3, 3) ∉ R so it is not reflexive relation.

(1, 3) ∈ R but (3,1) ∉ R, so it is not symmetric relation.

(iii) Reflexive and symmetric but not transitive.

Let a relation R is defined on a set A = {1, 2, 3}

Answer: {(1, 1), (2, 2), (3, 3), (1, 2), (2, 1), (1, 3), (3,1)}

(1, 1), (2, 2), (3, 3)∈ R so it is Reflexive.

(1, 2), (2, 1), (1, 3), (3, 1)∈ R so it is symmetric.

(3, 1)∈ R, and (1, 2) ∈ R but (3, 2) ∉ R so it is not transitive.

(iv) Reflexive and transitive but not symmetric.

Let a relation R is defined on a set A = {1, 2}

Answer: R = {(1, 1), (2, 2), (1, 2)}

(1, 1), (2, 2) ∈ R, so it is a reflexive relation.

(1, 2) ∈ R but (2, 1) ∉ R so it is not symmetric.

(1, 2) ∈ R  and (2, 2) ∈ R ⇒ (1, 2) ∈ R,  so it is a transitive relation.

(v) Symmetric and transitive but not reflexive.

Answer: Let a relation R is defined on the set A = {1, 2, 3}
Ans: A =  {(1, 1), (2, 2), (1, 2), (2, 1)}

(3, 3) ∉ R, so it is not reflexive relation.

(1, 2), (2, 1) ∈ R, so it is symmetric.

(1, 2) ∈ R,  (2, 3) ∈ R, ⇒ (1, 3) ∈ R ∀ 1, 2, 3 ∈ R  so it is transitive relation.

Functions 

Functions : Functions are those relations (or subsets) of cartesian product in which no two ordered pair have same first element.

If any two ordered pair have same first element, then the relation is not a function.

Number of elements 

If n(A) = n and n(B) = m, then number of functions from A to B = mⁿ

If n(A) = 3 and n(B) = 4, then number of functions from A to B = 4³ = 64

If n(A) = 4 and n(B) = 3, then number of functions from A to B = 3⁴ = 81

TYPES OF FUNCTIONS

There are mainly three types of function

1) One-One functions (or Injective functions)

2) Many one Functions

3) Onto functions (Surjective Functions)

4) Bijective Functions

One-One functions (or injective functions):

A function f : A →B is said to  be one –one or injective function if different elements of set A has different images in set B

Mathematically: 

Case 1: For all a, b ∈ A, we have: If  f(a) = f(b) ⇒ a =  b
Case 2 :  For a, b ∈ A, such that : If a ≠ b ⇒ f(a) ≠ f(b)

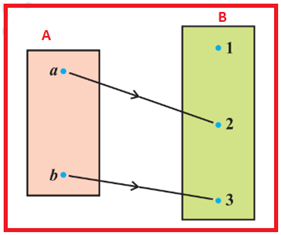
In the above figure different elements of set A have different images in set B. So this function is called one-one function.

Number of Elements in One-One functions

Case I If n(A) ≤ n(B)

Let set  A has n elements and the set B has m elements (n ≤ m). Then the number of injective functions that can be defined from set A to set B is  given by

 

If a function has 'n' elements and is defined from A to A then number of injective relations from A to A = ⁿP_n  = n!

If n > m,  then Then the number of injective functions that can be defined from set A to set B is = 0

Example

Set A has 3 elements and the set B has 4 elements. Then the number of injective functions that can be defined from set A to set B is  = ⁴P₃ = 4! = 24.

Many One functions:

If two or more elements of set A have same image in set B then it is called many one function.

If a function is not one-one then it is called many one.

Here two different elements a and b of set A has same image in set B. So it is not one-one function. It is only a many one function.

Onto function ( or surjective function)

A function f : A →B is said to be onto (or surjective) function, if every element of set B is the image of some element in set A.

Let y ∈ B, then for every  element  y ∈ B,  ∃ (there exist) an element   x ∈ A such that  f(x) = y.

Other definitions of onto functions are as follows

A function f : A →B is said to be onto (or surjective) function, if every element of set B has pre - image in set A.

If range of the function is equal to the co-domain(or set B), then it is called onto function.

In the above figure every element of set B is the image of some element in set A so it is an onto function. It is neither  many one nor   one-one.

Number of onto functions

Case I: If n(A) ≥  n(B)  or  n ≥ m

If n(A) = m, and n(B) = n, then number of onto functions from A to B is 

^mC₀(m)ⁿ - ^mC₁(m-1)ⁿ + ^mC₂(m-2)ⁿ - ^mC₃(m-3)ⁿ......… + ^mC_m-1(1)ⁿ 

Example 1

If n(A) = 6, n(B) = 3, then find the total number of onto functions

Solution

Number of onto functions from A to B are given by

 

= 729 - 3 ✕ 64 + 3 ✕1

= 540

Example 2:

If n(A) = 6, n(B) = 4, then find the total number of onto functions

Solution

Number of onto functions from A to B are given by

 

= 4096 - 4 ✕ 729 + 6 ✕64 - 4

= 4096 - 2916 + 384 - 4

= 1560

Case II : If n(A) <  n(B)  or  m < n 

If number of elements in set A is less than the number of elements in set B then there is no onto function possible.

Bijective Function

The functions which are both one-one (or injective) as well as  onto (or surjective) are called Bijective Functions

Number of Bijective Functions

If n(A) = n(B) = n,  then number of bijective functions from A to B is given by ⁿP_n  = n!

Example

If n(A) = 3, then number of bijective functions from set A to A are 3! = 6

If n(A) ≠ n(B), then no bijective function is possible

Summery of the Results

*****************************

Note: If a function is defined from set A to set B and n(A) = n and n(B) = m the we find the following results

n(A) = n, n(B) = m	n > m	n = m	n < m
No. of functions	mn	mn	mn
No. of one-one functions	0	nPn= n!	mPn
No. of onto functions	mC0(m)n - mC1(m-1)n + mC2(m-2)n …… mCm-1(1)n	mC0(m)n - mC1(m-1)n + mC2(m-2)n …… mCm-1(1)n	0
No. of Bijective Functions	Not Possible	nPn= n!	Not Possible

***************************************

Exercise 1.2

Q No. 9:

State whether the function f is bijective. Justify your answer.

Solution

One-One:  Let (1, 2) ∈ N then

 

f(1) = f(2) but 1≠2

⇒ f is not one one function.

Onto

Case 1: If n = odd = 2q+1=4q+1

 

⇒ 2q + 1 is also an odd function ∈ N

Case 2: If n = even = 2q = 4q, 

 

⇒ 2q  is also an even function ∈ N

From case 1 and case 2 we conclude that :

*For all odd numbers in the domain we have odd numbers in the co-domain .

*For all even numbers in the domain we have even numbers in the co-domain .

⇒ R_f = Odd natural number and Even natural numbers.

⇒ R_f = All Natural Numbers = Co-domain

⇒ f(x) is an onto function.

Now f(x) is an onto function but not one-one.

So f(x) is not a bijective function.

************************************************************************

Deleted Topics fro CBSE Syllabus

Composition of two functions

Let f : A →B and  g : B →C be two functions. Then the composition of f and g, denoted by gof, is defined as the function gof : A →C given by

gof(x) = g[f(x)],  ∀ (for all)  x ∈ A

Composition of two functions exists only if co-domain of first function is equal to the domain of second function

In the above figure function f is defined on the element of set A (i.e.  x), function g is defined on the elements of set B (i.e f(x) ) so composition from set A to set C becomes gof or g[f(x)]

Bijective functions:

The functions which are one-one and onto both are called bijective functions.

Invertible functions and existence of inverse

If a function f is one-one and onto then it is an invertible function.

If a function is an invertible function then inverse of f exist and is denoted by f^-1.

If f is invertible the f must be one-one and onto, conversely if f is one-one and onto  then f must be invertible. If f is invertible then f^-1 exists.

Let f(x) = y is an invertible function then f^-1 exists and we can write f^-1(y) = x

Example : f(x) = { (a, 1), (b, 2), (c, 3), (d, 4)}, this can be written as

f(a) = 1, f(b) = 2,  f(c) = 3,  f(d) = 4

If f is invertible then we can write

f^-1(1) = a,  f^-1(2) = b,  f^-1(3) = c,  f^-1(4) = d

If f and g are two invertible functions then their composition gof is also invertible.

Give an example of a relation which is

i) Symmetric but neither reflexive nor transitive

Ans  R = { (1,2), (2,1)}

ii) Transitive but neither reflexive nor symmetric

Ans:  R = { (1,1), (2,2), (1,2), (2,1), (3,4)}

iii) Reflexive and symmetric but not transitive.

Ans: R = {(1,1), (2,2), (3,3), (1,2), (2,1), (2,3), (3,2)}

iv) Reflexive and transitive but not symmetric.

Ans: R = {(1,1), (2,2), (1,2), (2,1), (2,3), (3,3)}

v) Symmetric and transitive but not reflexive

{(5,6), (6,5),(5,5) }

 THANKS FOR YOUR VISIT

PLEASE COMMENT BELOW